Calculating forces in wires by Lami's theorem./ Finding tension in wires using Lami's theorem.

 Eg:

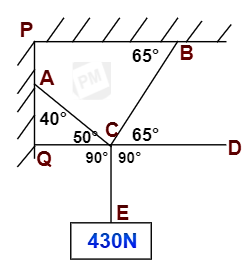
Calculate the tensional force developed in the wires  AC & BC in the following drawing using Lami's theorem.

To find:

The tensional forces  developed in the wires AC & BC

Calculation:

Let us draw a line QD parallel to the support PB as shown below. The line QD should pass through intersection point C.

As ∠ B = 65°, the ∠BCD will be equal to 65°

Note: 

The alternate angles of a line cutting the two parallel lines are always equal to one another.

 ∠Q =90° as line QD is perpendicular to the support QP.

In triangle AQC, 

∠C = [180°- ( ∠Q + ∠A )]

       = [180°- ( 90° + 40° )]

       = 50°

As an applied force is in the vertical axis, ∠QCE = ∠DCE = 90°

( As shown in the above drawing)

Now, let us draw a free-body diagram of forces as shown below.

∠ACE = [∠ACQ + ∠QCE]

            = [ 50° + 90°]

             =  140° 

(As shown in the above drawing)

∠BCE = [∠BCD + ∠DCE]

            = [ 65° +  90°]

             =  155° 

∠ACB =  [360° - (∠ACE + ∠BCE)]

 (As total value of a angle = 360°)

∠ACB =  [360° - ( 140° +  155° )]

             = 65° 

By applying Lami's theorem,

T1 / sin155° = T2 / sin140° = 430N / sin65°

Where, T1 & T2 are the tensional forces in wires.

Therefore,

T1 = [(430N ➗  sin65°) x sin155°]

     = [ (430N ➗ 0.906 ) x 0.422]

     = [ 474.613N x 0.422 ]

  T1 = 200.287N

T2 = [(430N ➗  sin65°) x sin140°]

     = [ (430N ➗ 0.906 ) x 0.643 ]

     = [ 474.613N x 0.643 ]

  T2 = 305.075N

Tensional force in wire AC = T1 = 200.287N

Tensional force in wire BC = T2 = 305.075N

     Thank you for going through these calculation steps❤. Have a good day 😄.

Share: