How to find the center of gravity of an L-section?/ Calculating centroid of an MS angle section.

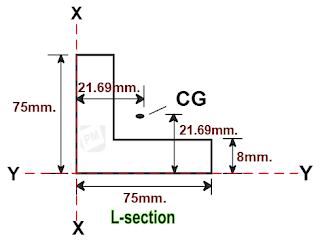
 Let us consider an angle- section or L-section as shown below.

Given data:

Depth of L-section = 75mm.

Width of L-section = 75mm.

The thickness of L-section = 8mm.

Calculation:

The given L- section is asymmetrical to both X-axis & Y-axis.

What does that mean?

Let us observe the drawing as shown below.

When we divide the L-section into two equal halves by drawing  X-axis, the two parts on either side are not identical and they have different masses. The same is true for the Y-axis.

Therefore the center of gravity does not lie on the central X & Y-axis.

Let us split the L-section into two rectangles ABCD & BEFG having the lines XX & YY as the reference axis.

The Axis of reference is the edge line that we take on the drawing. As CG does not lie on any symmetrical central axis, we have to calculate the position of CG from two reference axes.

Area of rectangle ABCD 

A1= [depth of rectangle ABCD × rectangle thickness]

    = [67mm. × 8mm.]

 A1= 536 mm2

Co-ordinate X1 from reference axis YY

  = [ thickness of rectangle ABCD ÷ 2]

 = [ 8mm.÷ 2)]

X1 = 4mm.

Co-ordinate Y1 from reference axis XX

  = [thickness of rectangle BEFG + ( depth of rectangle ABCD ÷ 2)]

 = [8mm. + ( 67mm.÷ 2)]

Y1 = 41.5mm.

Area of rectangle BEFG 

A2 = [width of rectangle BEFG × rectangle thickness]

    = [75mm. × 8mm.]

A2= 600 mm2

Co-ordinate X2 from reference axis YY

= [ width of rectangle BEFG  ÷ 2)]

= [ 75mm.  ÷ 2)]

X2= 37.5mm.

Co-ordinate Y2 from reference axis XX

= [ thickness of rectangle BEFG  ÷ 2)]

= [ 8mm.  ÷ 2)]

Y2= 4mm.

Now, the distance of the center of gravity ( Ӯ ) of the given L-section from reference axis XX

= [{(A1×Y1) + ( A2 ×Y2)} ÷ ( A1 + A2)]

= [{(536× 41.5) + ( 600 × 4)} ÷ ( 536 + 600)]

= [24,644  ÷ 1136]

 Ӯ = 21.69mm.

Now, the distance of the center of gravity (艾  ) of the given L-section from reference axis YY

= [{(A1×X1) + ( A2 ×X2)} ÷ ( A1 + A2)]

= [{(536× 4) + ( 600 × 37.5)} ÷ ( 536 + 600)]

= [24,644  ÷ 1136]

艾 = 21.69mm.

Note: 

1. Distance of X1, X2, & center of gravity 艾, is measured from the reference axis - YY.

2. Distance of Y1, Y2, & center of gravity Ӯ, is measured from the reference axis - XX.

Thank you for going through these calculation steps❤. Have a good day 😄.

Share: