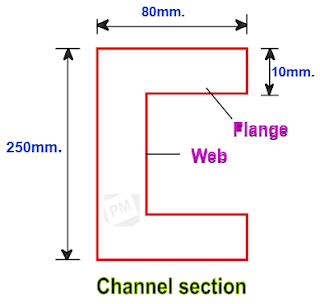
Let us calculate the moment of inertia about the centroidal axis for the C-section as shown below.
Given data:
Depth of C-section = 250mm.
Width of C-section = 80mm.
Thickness of C-section = 10mm.
First, you have to find the area of the rectangle ABCD, BEFG, & EHIJ, of the C-section. The center of gravity of the C-section should be calculated.
All these steps are already covered in a separate article as linked below.
👀. How to find the center of gravity of a C-section?
Area A1 of rectangle ABCD = 800 mm2
Area A2 of rectangle BEFG= 2300 mm2
Area A3 of rectangle EHIJ =800 mm2
CG of rectangle ABCD X1 = 40mm.
CG of rectangle BEFG X2 = 5mm.
CG of rectangle EHIJ X3 = 40mm.
CG of C-section 艾 = 19.36mm.
Note: All the values are taken from the above-linked article.
1. Moment of inertia of C-section about X-axis
Iₓₓ = [Ixx1 + Ixx2 + Ixx3]
Where Ixx1 👉 Moment of inertia of rectangle ABCD about X-axis
Ixx2 👉 Moment of inertia of rectangle BEFG about X-axis.
Ixx3 👉 Moment of inertia of rectangle EHIJ about X-axis
Let us draw the local axes X1X1, X2X2, & X3X3 passing through the CG of rectangles ABCD, BEFG, & EHIJ as shown below.
From the above drawing,
Y1 = [depth of rectangle EHIJ + depth of rectangle BEFG + 1/2 × depth of rectangle ABCD]
= [10mm. + 230mm. + 1/2 × 10mm.]
= 245mm.
Y2 = [depth of rectangle EHIJ + 1/2 × depth of rectangle BEFG ]
= [10mm. + 1/2 × 230mm.]
= 125mm.
As the local Y2 axis overlaps Y-axis, Ӯ = Y2 =125mm.
Y3 = [1/2 × depth of rectangle EHIJ]
= [1/2 × 10mm.]
= 5mm.
As all these three axes are parallel to the X-axis, we shall use the parallel axis theorem to calculate MI.
a. Ixx1 = [IG1 + A1h1²]
Where IG1 is the MI of the rectangle ABCD about its local X1-axis.
The formula for MI of rectangle = IG1= [ bd³ ÷12]
So, Ixx1 = [( bd³ ÷12 )+A1h1²]
Here, b = width of the rectangle ABCD = 80mm.
d= depth of rectangle ABCD = 10mm.
h1= [Y1 - Ӯ]
= [245mm. - 125mm.]
= 120mm.
Ixx1 = [( bd³ ÷12 )+A1h1²]
Ixx1 = [( 80×10³ ÷12 )+ {800 × (120)²}]
= [(6,666.67) + {11,520,000}]
= 11,526,666.67 mm4
= 11.527× 10⁶mm⁴
Similarly,
b. Ixx2 = [IG2 + A2h2²]
Where IG2 is the MI of the rectangle BEFG about its local X2-axis.
The formula for MI of rectangle = IG2= [ bd³ ÷12]
So, Ixx2 = [( bd³ ÷12 )+A2h2²]
Here, b = width of the rectangle BEFG = 10mm.
d= depth of rectangle BEFG = 230mm.
h2= 0
As the local X2-axis overlaps X-axis, the value of h2 becomes zero.
Ixx2 = [( bd³ ÷12 )+A2h2²]
Ixx2 = [( 10×230³ ÷12 )+ {2300 × (0)²}]
= [(10,139,166.67) + {0}]
= 10,139,166.67 mm⁴
= 10.139× 10⁶mm⁴
c. Ixx3 = [IG3 + A3h3²]
Where IG3 is the MI of the rectangle EHIJ about its local X3-axis.
The formula for MI of rectangle = IG3= [ bd³ ÷12]
So, Ixx3 = [( bd³ ÷12 )+A3h3²]
Here, b = width of the rectangle EHIJ = 80mm.
d= depth of rectangle EHIJ = 10mm.
h3= [ Ӯ - Y3]
= [ 125mm. - 5mm.]
= 120mm.
Ixx3 = [( bd³ ÷12 )+A3h3²]
Ixx3 = [( 80×10³ ÷12 )+ {800 × (120)²}]
= [(6666.67) + {11,520,000}]
= 11,526,666.67mm⁴
= 11.527× 10⁶mm⁴
2. Moment of inertia of I-section about Y-axis
Iyy = [Iyy1 + [Iyy2 + I yy3]
Where Iyy1 👉 Moment of inertia of rectangle ABCD about Y-axis
Iyy2 👉 Moment of inertia of rectangle BEFG about Y-axis.
Iyy3 👉 Moment of inertia of rectangle EHIJ about Y-axis
Let us draw the local axes Y1Y1, Y2Y2, & Y3Y3 passing through the CG of rectangles ABCD, BEFG, & EHIJ as shown below.
As all these three axes are parallel to the Y-axis, we shall use the parallel axis theorem to calculate MI.
a. Iyy1 = [IG1 + A1h1²]
Where IG1 is the MI of the rectangle ABCD about its local Y1-axis.
The formula for MI of rectangle = IG1= [ db³ ÷12]
So, Iyy1 = [( db³ ÷12 )+A1h1²]
Here, b = width of the rectangle ABCD = 80mm.
d= depth of rectangle ABCD = 10mm.
h1= [X1 - 艾]
= [40mm. - 19.36mm.]
= 20.64mm.
Iyy1 = [( db³ ÷12 )+A1h1²]
Iyy1 = [( 10×80³ ÷12 )+ {800 × (20.64)²}]
= [(426,666.67) + {340807.68}]
= 767,474.346 mm4
= 7.674× 10⁵mm⁴
a. Iyy2 = [IG2 + A2h2²]
Where IG2 is the MI of the rectangle BEFG about its local Y2-axis.
The formula for MI of rectangle = IG2= [ db³ ÷12]
So, Iyy2 = [( db³ ÷12 )+A2h2²]
Here, b = width of the rectangle BEFG = 10mm.
d= depth of rectangle BEFG = 230mm.
h2= [ 艾 - X2]
= [19.36mm. - 5mm.]
= 14.36mm.
Iyy2 = [( db³ ÷12 )+A2h2²]
Iyy2 = [( 230×10³ ÷12 )+ {2300 × (14.36)²}]
= [(19,166.67) + {474,282.08}]
= 493448.746 mm4
= 4.934× 10⁵mm⁴
a. Iyy3 = [IG3 + A3h3²]
Where IG3 is the MI of the rectangle EHIJ about its local Y3-axis.
The formula for MI of rectangle = IG3= [ db³ ÷12]
So, Iyy3 = [( db³ ÷12 )+A3h3²]
Here, b = width of the rectangle EHIJ = 80mm.
d= depth of rectangle EHIJ = 10mm.
h3= [X3 - 艾]
= [40mm. - 19.36mm.]
= 20.64mm.
Iyy3 = [( db³ ÷12 )+A3h3²]
Iyy3 = [( 10×80³ ÷12 )+ {800 × (20.64)²}]
= [(426,666.67) + {340807.68}]
= 767,474.346 mm4
= 7.674× 10⁵mm⁴
Thank you for going through these calculation steps❤. Have a good day 😄.















No comments:
Post a Comment