If you are looking for a readymade calculator for type-5 land, then click here.
For the calculation procedure, go through the following steps.👇
Now, let us go through irregularly shaped land or plot, having 5 sides, and let us calculate the area of this plot, by using mathematical formulas.
Type - 5:
Here, all 5 sides of the land are unequal in length & are not parallel to each other.
Given data:
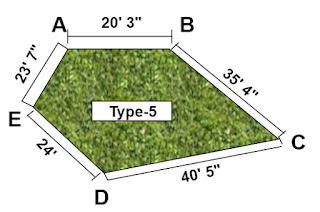
Side AB = 20' 3" = 20.25 ft.
Side BC = 35' 4" = 35.333 ft.
Side CD = 40' 5" = 40.416 ft.
Side DE = 24' = 24.0 ft.
Side EA = 23' 7" = 23.583 ft.
Note:
1. For your understanding, all the dimensions of the type-5 drawing are taken in ft. & in the first 4 types of land drawing, we have taken meters as a measuring unit.
2. We have converted all the land measurements into ft. by dividing inches by 12 (1 ft.=12 inch).
To calculate the area of 5-sided or pentagon-shaped land, we have to practically measure the distance between AD, & BD as shown in the above drawing.
Side AD = 40' 2" = 40.166 ft. as measured on-site.
Side BD = 43' 4" = 43. 333 ft. as measured on-site.
Note: You can measure the distance between AD & BD by plotting the land drawing on a proportionate scale, but the result may not be that accurate.
Now, we will calculate the area of triangle ADE, triangle ABD, & triangle BCD separately.
We will use Heron's formula to calculate the areas.
1. Area of triangle ADE
= √ s (s - a ) ( s - b ) ( s - c )
Here, s is the semi-perimeter of the triangle
i.e. s = [(a + b + c) / 2]
a, b, and c are the 3 sides of the triangle.
By data input
s = [(side EA + side DE + side AD) / 2]
= [(23.583 + 24 + 40.166) / 2]
= [87.749 / 2]
= 43.874 ft.
Area of triangle ADE
= [√ 43.874 ( 43.874 - 23.583) ( 43.874 - 24 ) ( 43.874 - 40.166 )]
= [√ 43.874 ( 20.291 ) ( 19.874 ) ( 3.708 )]
= [√ 65,604.812]
= 256.134 sqft.
2. Similarly, the area of triangle ABD
= √ s (s - a ) ( s - b ) ( s - c )
s = [(side AB + side BD + side AD) / 2]
= [(20.25 + 43.333 + 40.166) /2]
= [103.749/ 2]
= 51.874 ft.
Area of triangle ABD
= [√ 51.874 ( 51.874 - 20.25) ( 51.874 - 43.333 ) ( 51.874 - 40.166 )]
= [√ 51.874 × 31.624 × 8.541 × 11.708]
= [√ 164,043.103]
= 405.022 sqft.
3. Area of triangle BCD
= √ s (s - a ) ( s - b ) ( s - c )
s = [(side BC + side CD + side BD) / 2]
= [(35.333 + 40.416 + 43.333) /2]
= [119.082/ 2]
= 59.541 ft.
Area of triangle BCD
= [√ 59.541 ( 59.541 - 35.333) ( 59.541 - 40.416 ) ( 59.541 - 43.333 )]
= [√ 59.541 × 24.208 × 19.125 × 16.208]
= [√ 446,792.534]
= 668.425 sqft.
Now, the total area of land ABCDE
= [Area of triangle ADE + area of triangle ABD + area of triangle BCD]
= [256.134 sqft. + 405.022 sqft. + 668.425 sqft.]
= 1329.581 sqft.
Note:
By using Heron's formula, you can calculate the area of all types of irregular-shaped land or plots having an 'n' number of sides.
Thank you for going through this calculation❤. Have a good day😄












No comments:
Post a Comment